Some of the most confusing questions on the SAT math section are based on exponents. This is because intimidating questions can be made with exponents, which can be quickly solved by a student who knows them well.
The topic of exponents is an important one on the SAT, and exponents and square roots appear frequently. (See important topics on the SAT). Today we'll look at some of their fundamentals, as well as at common mistakes students make when dealing with exponents.
Today's article will serve as a jumping board for one of the question types we'll discuss later, complex exponent questions on the SAT.
What are exponents?
Exponents are values which show how many times to multiply a base. A base is the number being multiplied by itself.
Exponents are also known as powers. However, the word "power" can also be used to refer to the whole package, base plus exponent together.
Let's look at the following power and equation:

In the above equation, y is the base and 4 is the exponent. The exponent is sometimes known as the power, but "power" can also refer to the package of y to the 4th. For the purpose of clarity, that's how we'll use it in this article.
Exponent fundamentals
There are several important rules to remember when dealing with exponents. We'll do a brief review of each one, so that later we can move on to more complicated questions.
Product of powers rule
When multiplying like bases with respective exponents, keep the base and add the exponents.
That is:

Let's consider, for example, the following expression:

The final number is too large to be calculated on a calculator, but the phrase can be simplified. Note that the two things being multiplied have a common base. This is crucial, and the basis of a common mistake in regard to exponent calculations:
When the bases being multiplied are different, and their exponents are something other than 0 or 1, the expression can't be simplified.
Here, however, the base is the same. Following our rule, we'll keep the same base (4) and add the exponents. 17 + 5 = 22, hence:

Let's try another one. Let's look at the following expression:

Here, too, the base is the same. x + x = 2x, so the above expression should equal:

Let's look at one more example.

The base is the same, so we'll add the exponents.
x² + 3y - x² = 3y ⇒

This last example is reminiscent of some of the more complicated exponent questions we'll see on the SAT.
Let's move on to the next rule.
Quotient of powers rule When dividing like bases with respective exponents, keep the base and subtract the exponents.
That is:

As you may see, the quotient of powers rule is the exact counterpart of the product of powers rule. Note that the exponent of the denominator - in the equation above, y - is being subtracted from the exponent in the numerator, x. That is, the final exponent is x - y, not y - x.
Students sometimes get this confused.
Let's look at a few examples:

The base is the same - always important to check - so we'll subtract the exponents. 19 - 2 = 17, therefore:

Note that this is a large number. In the answer options it would likely be presented in this form (exponential) , rather than as a developed number.
Let's try one more example, this one with variables:

We'll subtract the two exponents. Note that the bottom exponent is negative, so be careful with parentheses:
2x - 4y - (-7y) = 2x - 4y + 7y = 2x + 3y
So:

Power of a power rule
When a number with an exponent is raised to another exponent, keep the base and multiply the exponents.
That is:

Let's see if we can understand the implications implicit in this, because this rule is a critical stepping stone in the solving of exponent questions on the SAT. Imagine that we're interested in the simplication of the following number expressed in exponent form:

The crucial point here is that 8 itself can be expressed as the power of another base:
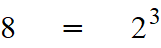
In that case,

Following the power of a power rule,

Whenever you see a number which can be expressed as a power of a smaller base, you can use the power of a power rule. On the SAT itself, this is almost an axiom:, when you can use this rule, you should use the rule.
When you can use the power of a power rule, you should use the power of a power rule.
The power of a power rule is frequently used in the opposite way as well, from right to left. Let's look at an algebraic question which works the opposite way:

In the equation above, we're moving from a smaller base to a larger base. It depends on what the question requires.
Power of a product rule
When raising the product of two or more variables by a power, that power can be distributed to each variable. That is:

This rule is fairly straightforward, so we'll just give a small example:

Power of a quotient rule
When raising the quotient of two variables to a power, that power can be distributed to each variable. That is:

The power of a quotient rule is the exact counterpart of power of a product. Again, we'll give a small example:

Power of zero rule A base raised to the power of 0 equals 1:
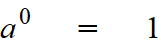
This is true for any base a, except for when a = 0. 0 to the zero power is undefined, but that usually doesn't crop up in the SAT.
Power of one rule
A base raised to the power of 1 equals that base:

This includes a base of 0.
Negative exponent
When you have a base with a negative exponent, take the reciprocal of the base, and make the exponent positive.
That is:

Please note that a negative exponent does not mean that the value of this number will be negative. If a base is positive, the power will always be positive - there is no exponent which can make it negative, or even equal to 0. This is a common mistake.
A power with a positive base will always be positive.
Let's look at an example:

The reason that 7 turns into 1/7 is because 7 is the same thing as 7/1. If you flip it, you'll get 1/7.
Note that according to the power of a quotient rule, the exponent of 2 is distributed to both the numerator and the denominator, resulting in 49.
Another example:

Note how in both examples, the first step is always to flip the base and make the exponent positive. Only then should you calculate / simplify. (In the last example, by cubing the 5 and 2.)
Fraction exponent rule
This rule relates to syntax. There are two different ways of writing fraction exponents, and you need to know how to move from one to the other. The rule looks as follows:

That is, the little exponent inside the radical is equivalent to simply writing the base with a new exponent. The exponent will be the reciprocal of the exponent inside the radical.
A more general equation would look as follows:

One way of thinking of this is that the base here isn't a , but rather a to the nth power. In that case, following upon the original simpler version of the fraction exponent we saw, we can use the power of a power rule to get this more general version.
Square roots
Square roots are a specific instance of fraction exponents. A classical square root is actually an inner exponent of 2. Because it's used so often, the 2 is usually dumped. That is, a square root is the equivalent of an exponent of 1/2:

So for example, the square root of 3 can be written in the following way:

Common mistakes students make regarding exponents
There are two common mistakes which lead to wrong answers on the SAT. We'll look at each one separately.
Mistake #1: Adding powers
Powers can often be simplified when multiplied. This is not true when adding powers. The sum of powers can't be simplified unless both the bases as well as the exponents of the two powers are exactly the same.
So for example, the following phrase:

cannot be simplified, though the bases are the same. The exponents are not the same, even if they both have an x.
Likewise with the following expression:

The exponents are the same, but the bases are different. This, too, cannot be added.
The only powers which can be added are, as mentioned earlier, ones with the exact same base and exponent. For example, the following equation is true:

You can think of a to the x power as its own variable, b.
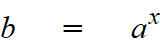
Plugging b's into the earlier equation, you'd get:

which is something that should be familiar to you. If you then plug in a to the x power again, you'd get the original equation.
Similarly, if a to the x power has a coefficient, this expression can also be simplified. For example:

Mistake #2: Squaring each radical in an expression separately.
Let's look at this expression for a moment:

One common mistake students make is thinking that the square of the sum of these parts is equal to the sum of the squares. Not true! That is:

This algebraic expression should be solved by using FOIL or the a² + 2ab + b² formula (more on this in a later article.) That will give you the true result.
A few notes
I realize that there are many rules here, and many names for rules which sound similar. Don't worry about the names; just practice.
Most of the rules are fairly straightforward, as I hope you can see. What really makes these questions confusing is when there's a combination of different rules, and there's a lot to do at once. However, solving these questions is still a fairly straightforward process. Just progress one step at a time.
In order to be able to deal with exponents on the SAT, I'd recommend first coming to know exponents well. There's one way to do this: obtain worksheets of challenging exponent problems and solve until you feel comfortable with the material. If there's a specific rule which you find especially tricky - many students are initially confused by the negative exponent rule, for example - train in that area until you feel confident.
Once you're comfortable with exponents, the supposedly "difficult" exponent questions on the SAT should no longer seem jarring, and you should be able to solve them quickly. We'll publish an article on especially confusing exponent questions in the near future, so keep an eye out.
In order to receive notifications when a new post is published, and keep up to date on the most effective ways to maximize your SAT / ACT score, try signing up to TovaKrakauerCoaching.com. It's totally free, and signing up takes two seconds: just click on the red sign-up button at the top of our home page, and enter your name and email.
For more tips and methods, or to get help personally tailored to your needs, consider working with me. I've helped people from all over the world get into their dream school. In coaching you, I adopt my methods specifically to your personality, schedule, and learning style. For this reason, studying privately with a skilled coach is the best way to increase your test score.
Happy learning,
Tova
.png)






















Comments